Updated on September 28, 2023
In poker, ICM stands for "Independent Chip Model". It helps a poker player at any stage of a poker tournament determine their current tournament equity. (How much money in the prize pool should currently be theirs.)
The calculation is based on how many chips they have presently relative to the total number of chips in play and the payout structure.
This information can be utilised to –
- Assist players in the decisions they must make during a hand while in a tournament, especially when they're towards the later or final table stages.
- Help determine how the prize pool is divided if a "chop" is agreed upon before the end of a tournament.
ICM CHART - What Factors Are Taken Into Account?
|
ICM considers: |
ICM does not consider: |
|---|---|
|
The chip stack's total size |
Size of blinds / Stack sizes in blinds |
|
Total # of chips in play |
Length of levels |
|
Number of Entrants |
Player Skill |
|
Payout structure |
Table position |
|
Number of remaining players |
Size of the tournament |
THE BASICS - How Does ICM Work in Poker?
The reason for using ICM in tournament poker is that the value of each tournament chip varies as each player gets eliminated and/or as payouts continue to increase. This situation is quite unlike cash games, where each chip amount is fixed and representative of the corresponding dollar amount.
In a cash game, if you double up, you double your equity, double your stack, and double your money. In a tournament, you could double up on the very first hand, but you still haven't doubled your tournament equity.
To use a simplified example to help show this, let's suppose we have a 10-man SNG with standard payouts: 1st gets 50%, 2nd gets 30%, and 3rd gets 20%. All players are given 1,000 tournament chips, meaning there are 10,000 total chips in play.
Before the tournament commences, ICM tells us that (with all players having equal starting stacks) all players have the same EV in the tournament of 10%. (Remember ICM doesn't take skill, table position, blinds, etc. into consideration. It's merely taking the number of chips a player has and relating it to the amount in play.
On the very first hand of this hypothetical tournament, Player 1 doubles up (seated in the big blind) and Player 10 busts (who was sitting in the small blind). Therefore, Player 1 now has 2,000 chips, and everyone else still has 1,000 chips.
Player 1 now holds 20% of the chips in play, but has he doubled his tournament equity from its original 10%?
No!
Why is this the case?
Due to the different structure of the prize pool, doubling up in chips won’t automatically double EV. Had this been a winner-take-all event, with 20% of the chips now in play, Player 1 would have a 20% shot at winning 100% of the prize pool. Therefore, his tournament equity would be at 20%.
However, in this tournament, the prize pool is divided up between 2nd and 3rd place as well. Therefore, the best that any player can do is to win a maximum of 50% total equity in the tournament -- 50% of the total prize pool. They also stand a chance of taking home perhaps 30% or 20% of the tournament's equity, if they place in 2nd or 3rd. It's for these additional placings that ICM is used to calculate a more accurate representation of one's tournament equity.
By using an ICM Calculator, we can see that Player 1's tournament equity is now at 18.44%. Therefore, while doubling his stack significantly increased his equity in the tournament from 10% to 18.44%, he didn't fully double this equity.
Why is this, and where did the remaining equity go?
The other eight remaining players received the extra tournament equity, gaining 0.19% equity from Player 10 busting. And they didn't even play a hand! This increase in equity makes sense, as there is now ONE less player to compete against with the same amount of chips in play.
NOTE: The payout amounts used for each place in the money (ITM) will also affect ICM and calculating tournament equities. Had it been a 1st-2nd-3rd setup with payouts of 65%-25%-10% of the total prize pool, Player 1's equity would have jumped to precisely 19% in repeating this same scenario!
This example, hopefully, goes to show why using ICM (instead of mere differences in players' chip stacks) is important in terms of calculating how a player's equity may fare – and at any given point in a tournament, relative to the number of chips that they have.

MORE ICM BASICS: Calculating ICM (Simple)
To help further illustrate why doubling one's chip stack doesn't double one's tournament equity (and also to help further understand the concept of ICM in tournament poker) consider this:
Two Players remain in a 6-man SNG, where each player started with 1,000 chips. The payouts are 70% for 1st and 30% for 2nd. Player 1 has a massive chip lead with 5,900 chips. Player 2 has a measly stack of 100 chips. After one hand, Player 2 manages to double his chips, meaning the stack sizes are now 5,800 and 200.
Did Player 2's tournament equity double by doubling his stack?
No, it hasn't.
With only two players remaining, each player is GUARANTEED 30% of the prize pool. This percentage represents the worst result each player could walk away with if they lose the tournament.
Therefore, players with any chips left are going to have somewhere over 30% equity in the tournament. As such, the two remaining players in this example would be competing for the remaining 40% of the prize pool. (Yes, the total amount for 1st is 70% of the prize pool, but because each player has at least 30% locked up, this leaves the remaining tournament equity up for grabs. And, the difference between 1st (70%) and 2nd place (30%) is 40%.)
As long as Player 2 still has chips, there is a small chance they could come back and win. They have a small portion of the equity in the remaining 40%.
Therefore, with only 100 chips, Player 2 would have a tournament equity of 30.67%. We arrive at this figure by taking the base equity they've already secured (30%) and adding that to their likelihood (based simply on the number of chips in their stack relative to the total number in play) of winning that remaining 40% equity:
= 30% equity guaranteed + ((100 chips/6,000 total chips) * 40% remaining tournament)
= 0.3 + (0.0167 * 0.4)
= 0.3 + 0.0067
= 0.3067
= 30.67% tournament equity
After doubling his chip stack from 100 to 200, we can use the same process to see that Player 2 would then have increased his tournament equity to 31.33%.
But, of course, not fully doubled it, as was posed in the original question.
How To Calculate ICM In Poker
As you can see, doubling one's stack in a poker tournament does not double one's equity. It's essential to know how to calculate ICM, so that you can make the corresponding decisions strategically, from hand to hand. (See later sections of this article.)
Also, so that you know how much each player should get if a "chop" situation ever arose at the final table. However, unlike in the previous section with players heads-up, calculations will get a little bit more complicated with more players added into the mix.
The way we calculate ICM manually in a scenario with multiple (3+) players remaining in a tournament is as follows. We take the number of chips a player has (relative to the total number of chips in play) and use this to calculate the likelihood of said player placing in each remaining spot in a tournament.
After this, we would relate these percentages to the corresponding monetary prizes associated with each spot and then add the results of all the outcomes together.
Let's use a real-life situation with the players and their chip counts taken from the start of Day 9 (3-handed play) during the 2019 WSOP Main Event in Las Vegas:
- Hossein Ensan - 326,800,000 (63.5% chips in play)
- Dario Sammartino - 67,600,000 (13.1% chips in play)
- Alex Livingston - 120,400,000 (23.4% chips in play)
Total chips in play: 514,800,000
NOTE: While a chop never occurred in this tournament, the following calculations are shown to illustrate how to do manual ICM calculations for a multiplayer chop.
With three players left, there were six possibilities for how the tournament could have concluded.
Those possibilities will be listed here in order of 1st, 2nd, and 3rd place:
- Ensan, Sammartino, Livingston
- Ensan, Livingston, Sammartino
- Livingston, Ensan, Sammartino
- Sammartino, Ensan, Livingston
- Livingston, Sammartino, Ensan
- Sammartino, Livingston, Ensan
For our ICM calculations, let's assume we're trying to find the ICM tournament equity for Hossein Ensan, the Day 9 chip leader. You'll notice that, in the above table, Ensan had two possibilities of placing 1st, two of placing 2nd, and two chances of placing 3rd.
To assist us in converting it all into ICM tournament equity, we'll need to determine the likelihood of him finishing the tournament in each place (based on current chip stack sizes).
Probability of Placing 1st - Options 1 + 2
With Ensan having 63.5% of the chips in play, there is a 63.5% chance that he will get 1st, based strictly on taking his current number of chips relative to the total amount in the game.
Probability of Placing 2nd - Options 3 + 4
For this section, we will have to calculate the options separately, to account for the two other player's probabilities of placing 1st ahead of him.
For option 3, Livingston has a 23.4% chance of coming in 1st. To determine the likelihood that Ensan will then come 2nd (between him and Sammartino), we must take (Ensan's chips/remaining players' chips -- in this case, Ensan's + Sammartino's).
This formula gives us the answer of 326,800,000 / (326,800,000 + 67,600,000) = 82.9%, meaning there's an 82.9% chance of Esan coming 2nd, if Livingston places 1st.
To determine the total likelihood of this option, we must now multiply these two possibilities together (Livingston winning and Ensan coming in 2nd): 0.234 * 0.829 = 0.194 = 19.4% chance this scenario will occur.
For option 4 in the table, we do the same calculations, but with Sammartino coming 1st (13.1% chance). Using the same maths formula 13.1% x (328.8 million / 447.2 million), we find that this result has a 9.6% chance of occurring, based on ICM and chip stacks.
Adding the likelihoods together of each scenario (19.4% and 9.6%), we see that there is a 29% chance of Ensan coming in 2nd place.
Probability for Placing 3rd - Options 5 + 6
The resulting likelihood of Ensan coming 3rd would be 7.5%. We arrive at this number by discovering there's a 4% of Option 5 occurring (23.4% * (67.6 million / 394.4 million)) and a 3.5% chance of Option 6 occurring (13.1% * (120.4 million / 447.2 million)).
NOTE: In the instance of calculating the likelihood of a final option of a scenario like this, you could also take 100% and subtract from it the results of the other options calculated (63.5% and 29.0% for 1st and 2nd, respectively) to arrive upon the final figure of 7.5% for Ensan's chances of placing 3rd, based on ICM.
Converting % into $ Using ICM

Using these percentages, we can then calculate the EV a player currently has in $$$ in a tournament, which is precisely what would be used to calculate payouts, if a situation to "chop" arose.
So, continuing with our example, here are what the Top 3 prize payouts were for the 2019 WSOP Main Event:
- 1st - $10,000,000
- 2nd - $6,000,000
- 3rd - $4,000,000
Here is the $EV Ensan has for finishing in each place:
- EV of 1st = 0.635 x $10,000,000 = $6,350,000
- EV of 2nd = 0.290 x $6,000,000 = $1,740,000
- EV of 3rd = 0.075 x $4,000,000 = $300,000
Adding all of these products together, we arrive at the total tournament EV of Hossein Ensan in dollars heading into Day 9: $8,390,000. Had the three remaining players chosen to do an ICM chop between themselves at the start of Day 9, Ensan would've won this amount of $8,390,000.
(Subsequent equities and $EV amounts could be calculated for the other two players using the same method as used above for Ensan.)
The Final Step: Calculating One's Equity with Multiple Players Remaining
As you can see, because the $EV amount for Ensan is less than the 1st place prize (as it will always be, when taking 2nd place, 3rd place, etc. into account), Ensan’s equity in the tournament wouldn't be that of his 63.5% of chips in play, but rather a total of 41.95%.
We arrive at that updated figure by taking his current EV in the tournament ($8,390,000) and dividing this by the total remaining money in the prize pool ($10m + $6m + $4m = $20,000,000).
ICM Formula for ICM Calculation
To summarise the previous section on ICM calculation, here is the step-by-step formula to use to calculate your tournament equity based on ICM considerations:
- Determine the size in chips of each player's chip stack
- Relate this to the total number of chips in play –
- Chip Stack / Total Chip
- This calculation will show each player's likelihood of WINNING the tournament.
- Determine the likelihood of all the different possibilities for how the tournament will end up (in terms of which place each player might get) -
- Determine all the different possible outcomes.
- Determine the likelihood of each outcome by starting with the probability the winner of each scenario will get 1st place.
- After this, to determine 2nd place likeliness, multiple winner's possibilities of winning (their chip share) by (2nd place chips/total remaining other chips, including 2nd place).
- To do this formula for more than three players, you must combine the likelihood of 1st and 2nd place (etc.) before calculating for a player in a later position.
- Relate these equities to the $ amount associated with the paid places to determine EV -
- Determine the EV in $ amounts for each scenario.
- Add them together.
- Divide this sum by the total remaining prize pool left to be awarded, to find any given player's current EV.
ICM Software for ICM Calculations
As shown in the example above, even with just three players remaining in a tournament, the amount of ICM calculations to do to calculate EV is already quite lengthy. (And at that, we were calculating the EV / ICM for only one player of those three in question!)
Imagine doing those calculations if play was 4-handed or 5-handed, or just after players got into the money! The number of combinations for each player would end up being incredibly time-consuming if done manually.
Therefore, because of the lengthiness and complexity of these calculations, it's not uncommon for players/poker rooms to use ICM software and ICM calculators - especially in the case of players looking to chop.
And it's not always required that you have a dedicated ICM calculator to do this! Even in database management software like PokerTracker4, basic ICM calculators have started to be included. There are websites where you can plug in the input values, and they'll spit out the ICM calculations. (For example, check out: https://www.icmizer.com/icmcalculator/, where you can calculate ICM values for up to 15 different players/payouts.)
Basic ICM calculators can be found as stand-alone or bundled applications on select mobile devices, too.
ICM Gameplay Considerations: Stack Sizes and ICM Pressure
Coming at ICM from a more strategic/gameplay perspective now, ICM pressure can come in many forms and various situations. Primarily, this term refers to the restrictions and alterations that a player must make to their hand ranges and/or how they play specific hands. Players don’t want to lose large amounts of equity in a tournament if they can at all avoid it, due to ICM and payout implications.
In fact, a lot of the strategy one should implement while playing a final table is related to ICM. It's extremely important to have an idea of how much your stack is worth at all times and make your bigger decisions with that in mind.
As a typical example, take a look at a common situation that comes up when ITM (in the money) in SNG's. Usually, there's always one player with each of the following stacks: 1 large stack, 1 medium stack, and 1 short stack.
For the example below, let's assume players have stack sizes of 3,000, 6,000, and 9,000 chips.
How these varying stack sizes should subsequently relate and adjust due to ICM pressure and considerations is pretty straightforward:
- As the medium stack, you don't want to get into epic confrontations with the big stack because this could cost you equity and/or your tournament life. You'd prefer to see the short stack bust out first (subsequently increasing your tournament equity) before you get too heavily involved in a big pot with the big stack. At the same time, the medium stack can take *some* chances against the short stack, although one must still exercise caution. While they won't bust and lose all their equity in the tournament if they lost an all-in to the short stack, it would likely leave them on the ropes, becoming the short stack.
- For the above reason, as the big stack, you can apply a great amount of pressure to both the medium stack AND the short stack, but especially the medium stack. They're handcuffed in between the likes of you and the short stack. They would rather preserve their tournament equity and potentially gain some if you're able to bust the shorter stack. And, while the short stack *could* put a small dent in your stack, even after they double through you, you'd still have considerable equity in the tournament.
- As the short stack, you have nothing to lose and everything to gain. You can risk getting involved in all-in spots and pots with any of the players, as you're generally looking for a full double-up. If you had a preference over who to choose to double through, it would be the medium stack, as this would knock him down most likely being the short stack. This scenario would boost your equity in the tournament even more than if you doubled through the big stack and the stack sizes were level again. (Stack sizes of 3,000, 6,000, and 9,000 would give the player with 6,000 chips 34% equity. If everyone's stack sizes were equal at 6,000, on the other hand, each player would have 33.3% equity. While the difference of 0.67% does not appear to be very substantial, it can still make noticeable differences to your long-term winnings and profit margins.)
ICM Gameplay Considerations: The Bubble
These "relative stack size" concepts don't only apply when there are three people left; they can also apply to the entire final table in an MTT (as there's usually a pay jump for each elimination), as well as when the "money bubble" is about to burst.
The bubble is a unique part of a poker tournament. Finish out of the money, and you've lost all tournament equity (and have nothing to show for it). Cruise past the bubble and not only do you get to continue playing, but you also have a minimum amount of tournament equity locked up, which will subsequently have a nice, profitable payday to go along with it!
ICM considerations are very prevalent during the bubble in a poker tournament. As such, short stacks during this time are usually seeking to avoid any confrontation and not go broke.
On the flip side, good big-stack players are going to be aware of this and look to exploit it by chipping up and applying pressure to everyone else, most specifically the short stacks.
In fact, on the bubble is where big stacks can look to increase their chip lead in heaps because everyone else is usually just trying to sail into the money quietly.
ICM Catastrophe: A Hand Example
One intense hand from the World Series of Poker 2010 Main Event Final Table shows the prominence of ICM considerations and how massive a detriment to one's tournament results they can be.
To set the stage, with three players left, here were the chip counts before the catastrophe of a hand began:
- John Racener - 36,450,000 (17% of chips remaining)
- Jonathan Duhamel - 88,100,000 (40% of chips remaining)
- Joseph Cheong - 95,050,000 (43% of chips remaining)
John Racener folded the button. Joseph Cheong raised to 2.9 million from the small blind with A♠7♥. Duhamel 3bet to 6.75 million with Q♣Q♦. Cheong 4bet to 14.25 million. Duhamel 5bet to 22.75 million.
And then... Cheong 6-bet RIPPED it for 95.05 million, having Duhamel covered!
Before we get to the results of the hand, let's briefly dive into analysing Cheong's decision to 6bet jam A7o :
- Cheong has an Ace in his hand, which helps reduce the number of Aces that Duhamel could have. (The possible combinations of AK or AQ are reduced from 16 to 12. It also halves the number of Pocket Aces combos that Duhamel could have from 6 to 3.)
- Cheong has a slight chip lead over Duhamel, which is undoubtedly significant. While both players have roughly the same tournament equity currently, if both players go all-in and Duhamel loses, then it's a pretty big deal. Primarily because of the current size of Racener's stack in comparison with both of them, as well as the subsequent equity he'd be forfeiting to Racener by busting.
In short, Cheong put Duhamel into a fascinating, highly pressure-filled spot. Yes, while there's probably a better selection of AX hands that Cheong could've ultimately decided to 6bet bluff shove with (either suited or wheel/connected combinations), it undoubtedly puts Duhamel to the test, especially when you factor ICM considerations into it (that Duhamel could bust behind Racener if he calls all-in and loses).
Now that said, in the long-term, is 6bet shoving A7o in this spot a +EV play? Probably not. (We'd have to abundantly dissect hand ranges, hand equities, and tournament equities to do this.) But, thinking long-term, this play may have cost Cheong millions of dollars in equity.
For the results of the hand, Duhamel called with his Queens – and they held. He had a commanding chip lead after that, with 176 million vs. Racener's ~36 million and Cheong's ~7 million.
Cheong busted shortly after in 3rd place, and Duhamel went on to seal his victory.

ICM Gameplay Considerations: Strategy and Theory
In cash games, if you're facing an all-in spot, to show long-term profit, you should:
- Calculate your pot odds and the equity you need to win the hand to make a profitable call.
- Determine your hand's actual equity against an approximate range of your opponent.
- Make the call if you have the appropriate odds (+chipEV call) OR fold if you have insufficient odds/equity for the spot in question.
For tournament situations, however, it's not always so cut and dry because of (you guessed it!) ICM considerations.
As an example, let's say that we're on the bubble of a 9-handed SNG (4 players remain). Everyone has equal stacks of 4,500. The blinds are 200/400, and there is a 25 ante, as well. The CO folds, the BTN goes all-in, the SB folds, and we look down at QJs in the BB.
- Is this a call based on ICM (the next player to bust leaves with nothing; everyone else makes the money)?
- How much equity is gained/lost by calling here?
Firstly, we must assume the button's pushing range, which could very well look something like this (42.87% of hands):
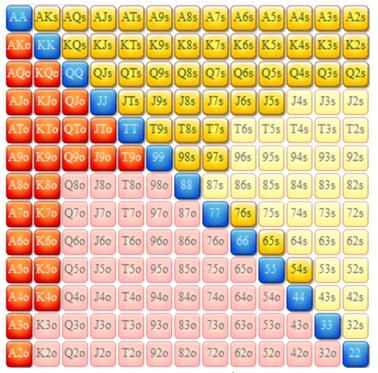
22+,A2+,K2s+,K4o+,Q2s+,Q9o+,J5s+,J9o+,T7s+,T9o,97s+,76s,65s,54s
Against this range, we can use an equity calculator to determine that QJs has 47.69% equity to win the hand, 3.10% to tie, and 49.21% equity to lose the hand vs. this range. With our big blind and ante already in the middle, we'd have to call off 4,075 chips more to win the 5,175 chips in the middle (small blind + big blind + antes + villain's shove).
In a cash game, we would simply determine, via pot odds, that we'd need 44.05% equity to call. Against the presumed button-shoving range of our opponent, our total equity (including tie possibilities) of 49.24% seems to be doing pretty well, meaning we should call...if this was a cash game!
Because this is a tournament (with subsequent ICM implications), the answer isn't so simple.
To determine whether we should call or fold in this spot in a tournament, we must figure out the tournament EV of each option! To do this, we must take the probability of each result (win, tie, lose), and multiply these by the chip EV that each result would bring (based on new chip stacks after the hand).
And then add them together to arrive at the total new tournament EV for making a call:
% Chance of Win/Loss/Tie Tournament EV (% of prize pool) after the hand
Win: 47.69% x 38.72%
Tie: 3.10% x 25.45% (chopping SB/antes of other players)
Lose: 49.21 % x 0%
By adding all of these results together, we can see that our tournament EV, based on ICM, if we called here would be 18.47% + 0.79% + 0% = ~19.25%.
Now we need to compare this to our tournament equity if we folded. After the hand, new stack sizes would be as follows (due to loss of blinds/antes):
- BB (Hero): 4075
- SB: 4,275
- BTN (Villain): ,5175,
- CO: 4,475
Plugging these stack sizes into an ICM calculator, we can see that our new tournament equity (as a result of folding) would be 23.47%. By calling QJs here, we'll lose an astonishing (23.47% - 19.25%) = 4.22% of our tournament equity (on average), which is quite considerable!
As a result, we can see how in a cash game based on pot odds and the same situation, this would be an easy call. However, with ICM implications in a 9-man SNG on the bubble, this QJs suddenly becomes an easy "toss in the muck."
NOTE: Notice how one marginally bad call (as illustrated here in this SNG example) can cause a 4.22% loss of tournament equity. Now imagine a similar situation with four players left at the final table at the WSOP Main Event! With about $23 million up for grabs in the last four spots (based on 2019's payout structure), 4.22% equity equates to a whopping $970,600 loss in monetary equity!
The purpose of saying this isn't to make you timid at the final table (i.e. with the potential to lose decent amounts of EV in certain spots). Instead, we want to emphasize how important it is to stay focused and think every decision through, especially when you're at a final table and/or big money is on the line.
ICM Software for ICM Practice: The Push/Fold Game
The payout structure of a tournament (in addition to relating one's current stack size to everyone else's) certainly helps determine what's going to be the most profitable way to play.
While the above examples show the tip of the iceberg for manual calculations, the good news is that software can help. Several programs have been developed to assist players in improving their push/fold game and overall gameplay for ICM spots like the above.
Mobile apps like SnapShove can help give you a starting point for improving your all-in-or-fold game. With customisable features like number of players, table position, effective stacks, antes and blinds, this will undoubtedly help you get the ball rolling in the right direction.

To take your game a step further, and also to incorporate such push/fold calculations specifically with ICM and payout considerations, ICMizer is a cool tool to look into that will help you do just that. (Available via computer web browser and for Windows download.) It will also help simplify more complicated calculations that would be very time-consuming if you had to do them by hand every time.
Looking back at our last example, we could've easily used ICMizer to show us the results in an instant!
Here we can see the probability of winning/losing/tying with QJs against the assumed Villain’s range:
Using these tools and software as part of your daily training will ultimately help you get to the point where you'll instinctively know how to make +EV plays based on ICM.
ICM Summary
Hopefully, this comprehensive guide has successfully shown you how to learn ICM poker and how to study it, too. While using ICM certainly isn't a perfect solution (i.e. as it doesn't take skill, player positions, who's posting their big blind next, etc. into consideration), it does allow players to have a baseline understanding of their current tournament equity.
By studying with the software recommended above (and perhaps by trying a few ICM examples of your own), knowing the Independent Chip Model will ultimately improve your gameplay.
It will also allow you to make more +EV decisions, and subsequently help you make more money at the felts in poker tournaments.
Originally Published on October 24, 2019


