In the modern poker world, poker solvers are a widespread topic of discussion. But what exactly are poker solvers, and how do they work?
In this introductory guide to poker solvers, we’ll discuss the following -
What is a Poker Solver?
A poker solver is a type of calculator that can generate “GTO” (Game Theory Optimal) strategies for the game of poker.
Solvers are currently extremely popular amongst online poker players and are available for purchase online.
The system requirements for running a poker solver are relatively minimal. Most modern home computers will have enough system resources to generate GTO strategies using a poker solver.
What is a GTO Strategy?
GTO stands for ‘game theory optimal’. A GTO strategy is an entirely unbeatable poker strategy that represents a mathematically perfect way of playing poker.

This concept might sound incredible at first, but there are some downsides.
- Firstly, GTO strategies are challenging to implement accurately.
- Secondly, GTO strategies don’t necessarily represent the best way of playing poker in any given situation.
Why? GTO strategies don’t actively take advantage of specific mistakes that our opponents are making.
Despite the downside of GTO strategies, working with a poker solver is a great way to improve our understanding of poker and develop into a strong player.
Using a Solver
The steps to using a poker solver may vary slightly depending on the software. But the basic process remains the same:
- Build a game tree (see What is a Game Tree below).
- Input ranges for the players involved (see Selecting Ranges for the Solve below).
- Run the solve and explore the results (see Using Solver Output below).
Getting up and running with our first solve is not that difficult. Ultimately, the skill lies in building logical game trees, selecting logical ranges, and interpreting the output in a relevant way.
Advanced poker players sometimes use a solver feature known as ‘scripting’ to queue up lists of related poker solves. This setup allows them to leave their computer running (perhaps overnight) to complete the list of solutions.
What is a Game Tree?
A game tree is a simplified representation of all the possible actions that may occur in a hand of poker. The individual points on the game tree where decisions occur are called decision nodes.
Example: Game Tree:
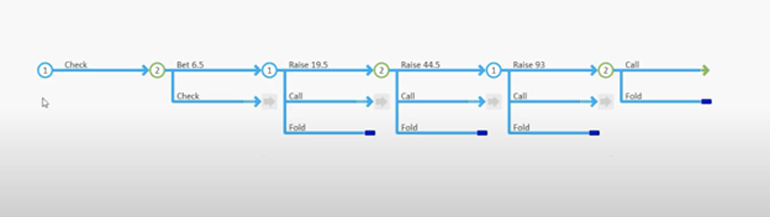
Solvers generally offer a game tree builder, which speeds up building a game tree by letting the user set various options.
Example: Game Tree Builder
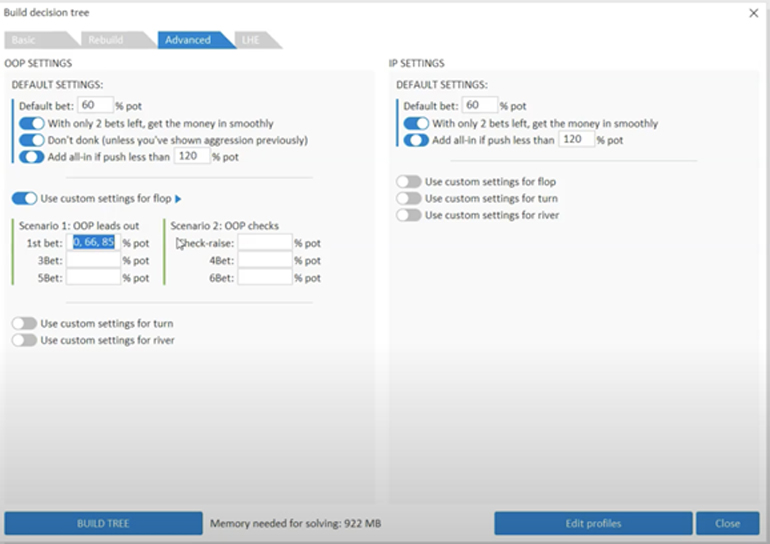
The result of the poker solve will be highly dependent on the quality of the game tree. If the game tree is a poot design, then the output will not be as relevant to the games we play.
We might wonder why the game tree needs to be simplified. Why can’t it just offer every possible action at every individual decision node?
The problem here is that the tree would be unmanageably large. If we were to use such game trees, it would take an unrealistic amount of time to solve anything.
Selecting Ranges for the Solve
Once the tree has been built, we then need to input hand ranges for the players involved in the hand. The user will usually get a hole cards grid selector, which can be used to add cards to each player's range.
Example: Starting Range Editor
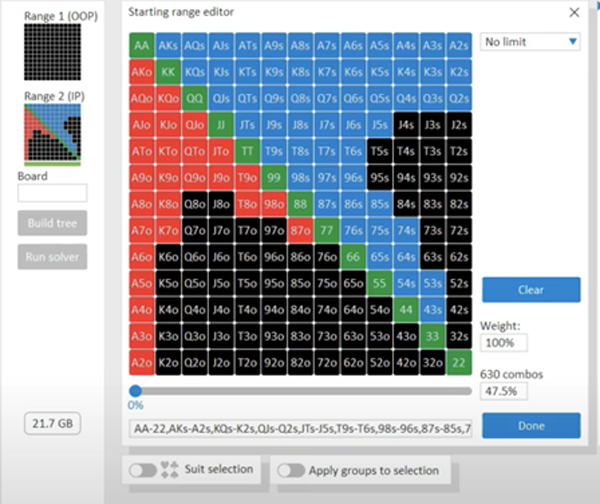
There is not necessarily a right or wrong answer when choosing which ranges to use for the solve. But this is not to say that some approaches aren’t better than others.
Here are some common approaches to selecting ranges:
- Using experience. Inputting ranges for each player based on our own experience of which types of hands players commonly show down, depending on the scenario. The downside here is that we could be way off with our estimates.
- Using ‘solved’ GTO ranges. Using GTO preflop ranges, created in a separate preflop solve. (See Running Preflop Solves below.)
- Using population ranges. Assuming we have many hands in a database, it’s possible to analyse the data to see which types of hands our opponents have shown down historically. This method might arguably be the most helpful way of doing things. But it’s hard to derive accurate information without vast sets of hand history data.
How Does the Solve Work?
So how does the solver work once we have everything in place and click the solve button?
The solving algorithm is an iterative process. So, it runs the same process repeatedly, gradually refining the strategies each time.

Eventually, the solver reaches strategies with no incentive for either player to deviate from their current strategy. In game-theory terms, this point is a Nash equilibrium and means that the solve is now complete.
In most cases, it will take too long for the solver to keep running until it reaches a perfect Nash equilibrium. The solver allows the user to set an appropriate level of accuracy slightly short of the true Nash equilibrium.
- The downside to this is that the results will be slightly inaccurate.
- The upside is that these inaccuracies are tiny, and it will be possible to complete the poker solve in a much shorter space of time.
A Closer Look at the Algorithm
Want the technical details? The following is a quick overview of how the solving algorithm works under the hood.
- Since the solver doesn’t know how to play poker, an arbitrary (random) strategy for both player 1 and player 2 is selected.
- The solver adjusts player 1’s strategy to a small degree so that it is exploiting the weaknesses in player 2’s strategy and generating higher profits.
- The solver then adjusts player 2’s strategy to a small degree so that it exploits the weaknesses in player 1’s strategy and generates higher profits.
- The solver then adjusts player 1’s strategy again, followed by player 2’s strategy in precisely the same way.
- As the process continues, both strategies become more and more refined until, eventually, neither strategy will be able to exploit the other by adjusting. We have reached a Nash equilibrium.
Using Solver Output
Solver output is pretty complex, and it is nearly impossible for a human player to use the strategies directly at the poker table.
One reason for this is that GTO poker strategies make heavy use of what are known as mixed strategies. The correct strategy for a particular hand may be mixed between different options.
For example, a specific hand might require a raise 17% of the time, call 63%, and fold 20% of the time.
Example: Mixed Strategy Solver Output
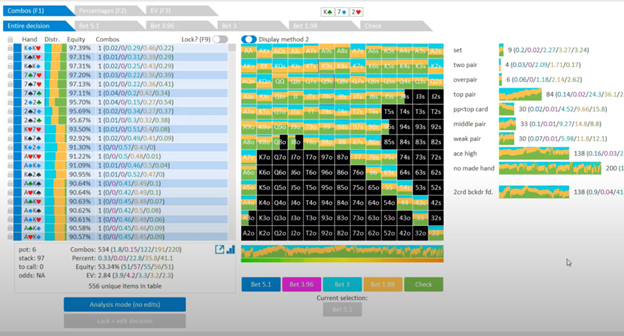
- One approach is to use solver output to help us learn about various poker concepts rather than attempting to implement GTO strategies directly.
- Another approach is to invest time in heavily simplifying solver output before using the strategies in-game.
Running Preflop Solves
It’s possible to use poker solvers to generate GTO preflop ranges. When running a preflop solve, providing the solver with ranges is unnecessary since we hope to get this info from the solve itself.
Likely, most of the solver work we do will only involve postflop solves. The downside in solving for preflop ranges is that the process is a lot more intensive and requires significantly more powerful hardware.
While a postflop solve can run on an average home computer, a preflop solve will likely require a very powerful custom system. Although it’s possible to build such a system at home (at quite a cost), a common approach is to rent a powerful cloud system for a period of time.
Since the average player does not have the knowledge or resources to run a preflop solve, a common approach is simply to buy a set of pre-solved preflop ranges. It is even possible to find complete sets of solved preflop ranges online for free in the modern poker era.

Solved preflop ranges can improve our preflop strategy, and we can input them into our solver for running postflop solves.
What Are Pre-Solved GTO Solutions?
When a company offers “pre-solved GTO solutions”, they give their users the solver output directly. The user won’t need to get their hands dirty building game trees and leaving their computers on to process solves.
- The upside to this is a quick and easy way to access large amounts of GTO poker solutions without waiting for solves to finish.
- The downside is that these services come at a price, typically a hefty monthly subscription fee.
In the long run, it’s usually significantly cheaper to run our own solves rather than relying on pre-solved GTO solutions.
Of course, we’ll naturally have to invest more time when running our own solves.
What is a Neural Network?

It’s worth giving a quick shout out to neural networks since they often crop up in conversations about poker solvers.
A neural network is not technically a poker solver. But both neural networks and solvers have the same ultimate goal: to calculate GTO solutions in various poker scenarios.
- A neural network does this by leveraging the power of machine learning. It plays trillions of poker hands against itself while slowly improving. In other words, it teaches itself how to play poker through trial and error and then stores those strategies for future reference.
- A solver has no existing database of strategies. It approaches each poker scenario by running the iterative algorithm discussed above.
It’s a calculator that does not know how to play poker. But it can derive Nash equilibrium strategies when fed with the correct information.
Getting Started with Poker Solvers
Price tags on solvers vary quite dramatically despite many of them using surprisingly similar algorithms under the hood.
It’s possible to find a free GTO solver that performs arguably as well as a commercial poker solver with a $1,000 price tag. Take your time to explore options and shop around.
If any of the above information seems abstract, the fastest way to learn is to get started by running your first solve and seeing how everything works.
You’ll then have taken the first step to become a much stronger poker player!


