Hand Combinations in Poker – Explained

Ever had that sinking feeling, facing a big bet on the river while holding a bluffcatcher? Perhaps we realise that there is some sort of process that we should be following but we find our mind going completely blank.

So how is it that good players seem to make consistently good decisions when facing a lot of action? Could it be that we are missing part of the puzzle here?

This is where knowledge of poker combinations comes in. Understanding poker combinations can help us to make better estimates regarding how often our holding is likely to be good. In this article we’ll consider the following -

Table of Contents

What Are Combinations?

There are two slightly different topics with the same name. 

The definitions are as follows:

Combinations– Meaning

1. A singular instance of a certain poker hand (usually referring to the hole cards).
2. Mathematics. A selection of items from a collection where order doesn’t matter.

Hand Combinations in Poker

The term “combination” (or “combo” for short) refers to the different ways we can make a specific type of poker hand.

Example: We are dealt AK preflop in Hold’em. How many different combinations of AK are there?

If we were so inclined, we could list every possible way of making AK. But most players remember that there are 16 combinations of every unpaired hand –

12 are off-suit, and 4 are suited.

Example: We are dealt 66 preflop in Hold’em. How many different combinations of 66 are there?

Once again, we could list all the possible combinations of 66. But it’s far easier to remember that there are 6 combinations of every pocket pair in Hold’em.

Calculating Combos in Hold’em

It’s easy enough to remember preflop combos. But things get a little more complicated when we need to take in to account card removal effect. (Various board cards are known, reducing the available combinations of different types of starting hand). 

It’s helpful if we have a system for calculating combos. 

Let’s start with unpaired hands.

Combos of Unpaired Hands:

Card 1 : Number of available cards * Card 2: Number of available cards

Returning to our AK preflop we can now see how our value of 16 was calculated. 
In a standard deck, there are 4 available Aces and 4 available Kings.

Therefore:   4 * 4 = 16 total combos of AK

Let’s see a slightly tougher question where we need to take into account card removal effects.

Example: In Hold’em, the flop texture is Ac8d7h. How many combinations of AK are there?

The key to this question is understanding that there are now only 3 Aces left in the deck. One of the Aces is clearly on the flop. 

As such, we have 3 available Aces and 4 available Kings.

Therefore: 3 * 4 = 12 total combos of AK.

Ok, now let’s learn the rule for pocket pairs.

Combos of Unpaired Hands:
Number of Available Cards * (Number of Available Cards -1)

------------------------------------------------------
                              2
 
Returning to our preflop question with the pocket 6s, four Sixes are available in the deck.

Therefore: (4 * 3) / 2 = 6 combinations of pocket Sixes. 

Let’s again see a slightly tougher question where we need to account for card removal effects.

Practice Questions with Combos

We should now be equipped to answer slightly more advanced questions regarding combinations. We’ll need basic arithmetic skills and some common sense. 

Example: We hold pocket Aces preflop. How many combinations of QQ+/AK does our opponent have?

Let's ignore the card removal effect temporarily. We know our opponent would have the following:

QQ+ = 18 combos (6 * 3)
AK = 16 combos
- for a total of 34 combos. 

However, our opponent holds two of the Aces meaning that the number of combos will be affected due to card removal effects. 

This scenario is sometimes referred to as the “blocker effect”. The QQ and KK combos will remain at 6 combos each, but the AA and AK combos will be affected.

One combo of Aces is left in the deck since we hold two of the Aces already.

(2 * 1) / 2 = 1 combo of Aces

There are 8 combos of AK (since there are 2 Aces and 4 Kings available)

4 * 2 = 8 combos of AK

So, if we list all the combos, we get the following:

AA – 1 combo
KK – 6 combos
QQ – 6 Combos
AK – 8 Combos
for a total of 21 combos. 

How many different ways of making a set are there?

It’s generally good to remember that there are always 3 combinations of each set available. That’s a total of 9 combinations of sets.

Let’s try something slightly more challenging.

Example: In Hold’em, the flop texture is Ac8d7h. How many different ways of making top pair are there?

This situation is where logic and common sense come in. We know that there are 12 combos of any individual top pair type hand such as AJ (4 * 3 = 12). 

But how many different Ax hands are there that make top pair?

There are 13 card ranks in a deck. So if we exclude AA, A8 and A9, 10 different types of Ax hand remain that make top pair, each with 12 combinations. 

That’s a total of 120 (10 * 12) different combinations of top pair on this texture.

Combinations in Mathematics

Now let’s visit our second definition of the term combinations. 

Mathematics: A selection of items from a collection where order doesn’t matter.

So far, we have seen ways of calculating hole card combinations. This second definition will help us calculate the probability of various board runouts. 

Let’s rewrite our definition to make it poker related -

Poker: A selection of cards from the deck where order doesn’t matter.

Let’s start with an example question. 

It’s often said that there are 19,600 different possible flops in Hold’em. 

Prove this mathematically using combinations.

Let’s start by looking at the mathematical formula for combinations.

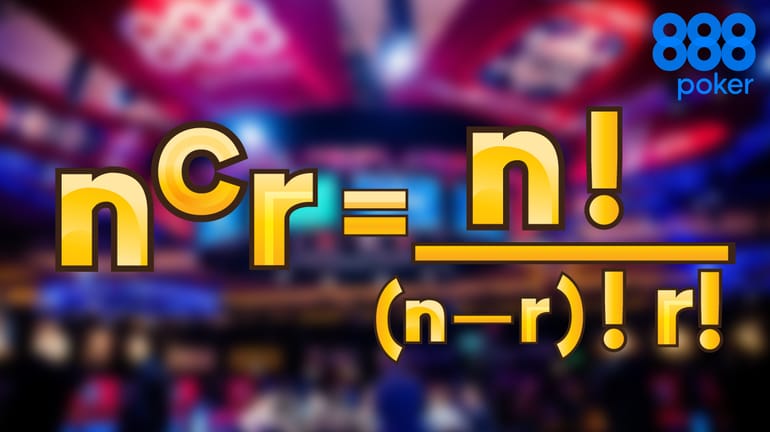
Let’s define the values in the formula -

n = total number to choose from (i.e. the number of cards in the deck)
r = total number we are choosing (i.e. how many cards we draw from the deck)
C = stands for combinations
! = mathematical function known as “factorial”. (e.g. 5! Is 5 * 4 *3 *2 *1)

Let’s assign values to n and r -

n = 52 because there are 52 cards in the deck.
r = 3 because we are drawing 3 cards to generate a flop.

Now plug our numbers into the formula –

52! 
-----
(49!) * 3!

It’s possible to plug these numbers directly into a calculator (using appropriate brackets). But it’s also viable to simplify the formula manually. 

Although the simplification method is slightly outside the scope of this article, it’s not overly complicated. We can simplify the above formula to the following –

52 * 51 * 50
-----------------
6

The result is 22,100 possible flop combinations. Interesting. So why is it that a quick online search reveals 19,600 possible flop combinations? 

Could it be that those calculations adjusting for the two often known (i.e. our hole-cards)? 

Let’s rerun the calculation -

n = 50 because 50 cards are remaining in the deck after our hole cards are dealt. 
r = 3 because we are drawing 3 cards to generate a flop.

This time we get –

50!
-----
47! * 3!

Which simplifies to:

50 * 49 * 48
------------------
6
- which equals 19,600!

So, when players say there are 19,600 flops, they mean assuming 2 cards from the deck are known. We’ve learned that there are 22,100 different flops that an outside observer would experience. (That’s as long as he doesn’t know any of the hole cards).

Let’s use our knowledge of combinations to see if we can answer a slightly more advanced question.

Example: We are dealt ThJh in Hold’em. What are our chances of flopping a flush?

We already know how many different flops there are (19,600). So our next goal is to establish how many ways of making a heart flush exist. This calculation assumes there are 11 hearts left in the deck. 

How can we establish the number of different 3-card combinations from a selection of 11 cards? 

Once again, this calculation is precisely what mathematical combinations are designed to do. 

n = 11 because this is how many hearts there are left in the deck assuming we already hold 2hearts in our hand.
r = 3 because this is the number of cards used to generate a flop in Hold’em.

Let’s input the numbers into our formula – 

11!
----------
8! * 3!

- which simplifies to

11 * 10* 9
---------------
6
= 165 ways of 3-heart flops being dealt.

The probability of flopping 3 hearts is, thus–

165 / 19,600 = 0.0084 or 0.84%

When we check with equity calculation software, it tells us that the chance of flopping a flush is 0.82% rather than 0.84%. 

Can you see what the discrepancy is?

Some of those three heart flops give us a straight flush. We need to know how many so that we can discount it from our total number of flush flops.

Flops that make the straight flush with ThJh–

AhKhQh
KhQh9h
Qh8h9h
7h8h9h

That’s four different flops that we need to discount from our current total of 165.

161 / 19,600 = 0.0082 or 0.82%

There we go. We have arrived at 0.82%, the same value given to us by equity calculation software. 

Let’s try one more.

Example: We are dealt AKo, what are our chances of flopping a straight?

Perhaps we are starting to see a pattern for the simplified version of the formula.

The pattern is as follows –

Numbers of Card 1 * Numbers of Card 2 * Numbers of Card 3
-------------------------------------------------------------------------
3!

In the case of attempting to make a straight, we need to hit a TJQ flop (although the order of the cards doesn’t matter). 

• There are 12 ways we can hit either a T, J or Q on the flop.
• There are 8 ways we can hit either a J or Q assuming we hit a T on the flop.
• Regardless of the flop card, 8 ways of catching part of the straight on the turn exist.

There are 4 ways we can catch the straight completing river card.

12 * 8 * 4
---------------
3!

If we multiply the top half of the formula (12 * 8 * 4), we get 384. This solution is the number of different ways of flopping the straight assuming the order of the cards is relevant (which is not).

So, 384 would suggest that TcJhQd and JhTcQd are different flops,which they are not for the purposes of this calculation. 

The mathematical name for a selection where the order matters is permutation rather than combination. It involves a slightly different formula.

The second part of the formula (divide by 3! Or 6) is used to account for duplicate flops (where just the ordering is different). 

384
------
6
= 64

That leaves us with 64 different ways of making a straight where the order of flop cards doesn’t matter.

Therefore: 64 / 19600 = 0.003265 or 0.33%

Using combinations to answer this question is not strictly necessary. We can confirm the answer by using the basic probability formula. 

Let’s see how it works –

1. Event 1 – First flop card is either a T, J or Q = 12/50 because 50 cards remain in the deck.
2. Event 2 - Second flop card is one of the remaining 8 cards to complete a straight = 8/49 because 49 cards remain in the deck.
3. Event 3 – Third flop card is one of the remaining 4 cards to complete a straight = 4/48 because 48 cards remain in the deck.

Now, we multiply the probability of each successive event to establish the total probability.

12/50 * 8/49 * 4/48 = 0.003265

Look familiar? 

That’s the same value we calculated earlier for flopping a straight given that we are dealt AK preflop.

Should we call or fold?

Well, according to our pot odds we need to win at least 33% of the time justify a call when facing a pot-sized bet. 

Can we expect to win that often? We aren’t left in the dark in this case.

Do we Have the Winning Combination?

Even with a strong idea regarding the number of hand combinations our opponent has, it’s almost impossible to know for certain whether we hold the winning combination. We’d only know for sure if we held the stone cold nuts (and even then we could sometimes chop). 

So if we don’t know for certain whether we hold the winning combination, how exactly do poker combinations help us with difficult bluffcatch decisions?

Here is a quick example of the type of analysis that can be run with combinatorics.

We hold a bluffatcher on the river when facing a pot-sized bet. We estimate that our opponent has around 40 combinations left in his range, 15 of which are bluffs, the other 25 being value combos. Should we call or fold?

Well, according to our pot odds we need to win at least 33% of the time justify a call when facing a pot-sized bet. Can we expect to win that often? We aren’t left in the dark in this case. Based on our estimates regarding the number of villain’s winning combinations we expect to have the best hand 15/40 or 37.5% of the time. 

Although we hence expect to lose the majority of the time when calling, this should mathematically be a winning decision in the long run and we should make the call. The stronger our awareness of villains combinations the more accurate and profitable our decisions will become.

Hand Combinations Summary

The most commonly used type of combinations is the hand combinations discussed earlier. We should generally assume that this is what a player wants to discuss on the topic of combinations.

In contrast, far fewer players know about mathematical combinations. The average player may not even have heard of them, let alone know how to calculate them. 

We’ve learned that there are 19,600 different flops, given two known hole cards. We can use combinations to establish how often certain types of flop hit. Then divide the result by 19,600 to learn the respective probability.

Having a firm grasp of such mathematical concepts can give us a significant edge over the playing field. 

Check out our web story about hands combination in poker.