Combinatorics in poker refers to the precise number of combinations of various player hands in a given situation.
- Paired hands will have 6 combos making up each holding:
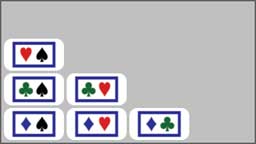
- Unpaired hands will have 16 combos that make up each holding:
- 4 of these combos will be suited: 1 each for diamonds, clubs, spades, and hearts.

- 12 of these combos will be unsuited (containing cards of different suits)

- 4 of these combos will be suited: 1 each for diamonds, clubs, spades, and hearts.
In this article, we will help you with learning combinatorics in poker, expanding on the following topics:
Why Combinatorics Is Essential in Poker?
Many people say that poker is a maths-based game. And to a great extent, that is undoubtedly true!
So, knowing and understanding combinations in poker will help you significantly develop the maths side of your game:
- Help you better understand poker ranges.
- Help you get a grasp on minimum defence frequency (MDF). You’ll get a greater understanding of the correct frequencies for calling, folding, and raising (depending on bet size).
- Help you to understand the likelihood of your opponent holding specific hands.
- Help you have a better understanding of the game overall.
Let’s dive in further!
How Many Hand Combinations Are There?
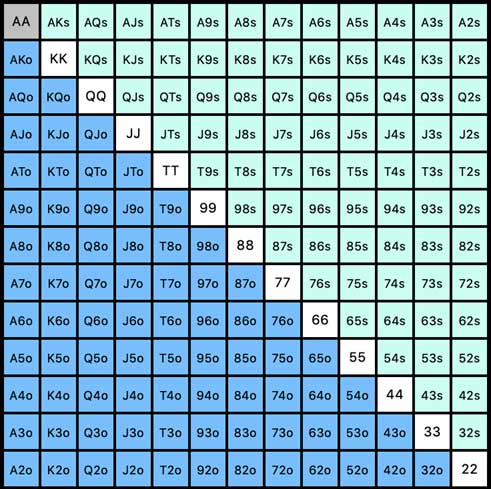
As you can see by the following grid, there are 169 different poker hands:
- Paired Hands represented by the white diagonal line (including Aces) from the top-left to the bottom-right corner.
- Suited Unpaired Hands represented by the hands in the upper-right quadrant of the chart (all hands in cyan)
- Unsuited Unpaired Hands represented by the hands in the lower-left quadrant of the chart (all hands in blue)
Now, look at the following grid, which lists the hands again. Let’s include the number of corresponding combinations for each poker hand.
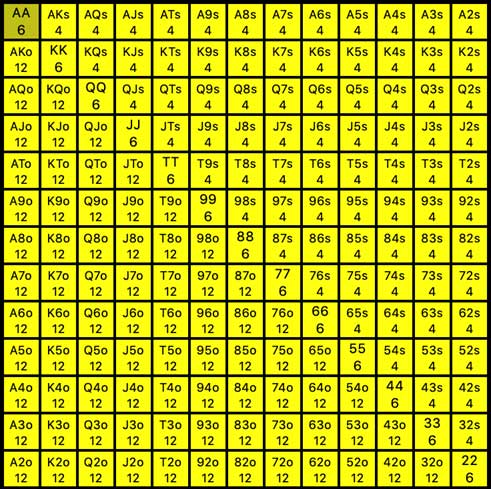
Based on the above charts, we can determine the following information using poker combinatorics:
- 78 combinations of paired hands
- 312 combinations of suited unpaired hands
- 936 combinations of unpaired unsuited hands
These figures add up to 1,326 different combos of poker hands that a player can be dealt!
Combinatorics and Hand Range Charts
Knowing this, we can better understand a lot more in poker. For example, with building ranges, we can now use combinatorics in our calculations.
- We can arrive at proper visual representations when trying to account for X% of hands in a range.
For example, let’s look at one possible opening range from the Button in a 100bb 6max cash game:
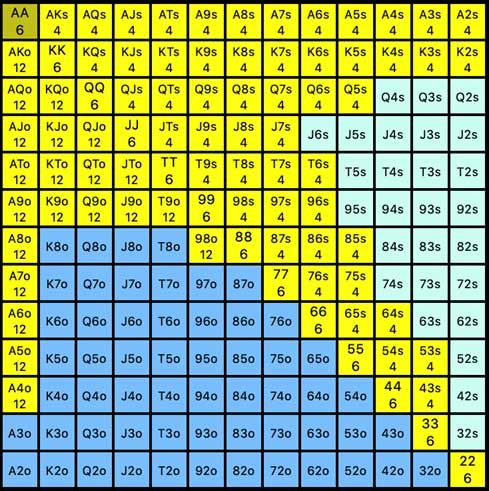
Counting the combinations of the various hands in the range, we can see that there are 534 different holdings highlighted. (There’s also a part in the poker software we use that tells us this.)
Knowing that there are 1,326 total possible holdings, the above starting hand range represents 40% of our starting hand range!
Let’s try another example. What might 80% of hands look like? (This percentage is a typical Small Blind open strategy in heads-up poker.)
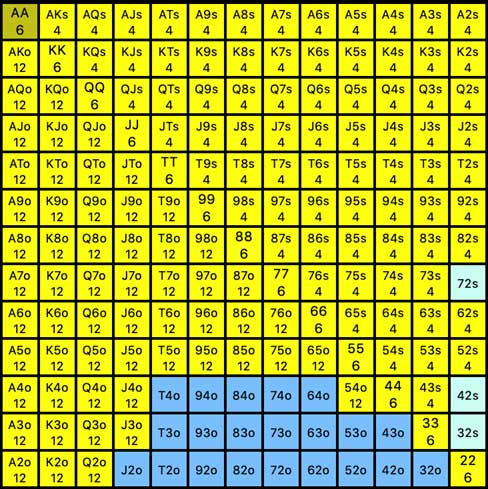
How does this knowledge impact you moving forward?
Using Combinatorics at the Bottom of Hand Ranges
What general % of hands should we usually open from each position when action has been folded to us? The answers should be common knowledge - 15% UTG, 40% from the BTN, etc.
But what exact hands you want to make up this % is (to an extent) up to you!
Of course, you’ll open all the strongest hands each time. But towards the bottom of the opening range, you can exercise a little bit of creativity:
- Do you want more pocket pair combinations included?
- Do you want many more suited hands than unsuited hands?
- Do you want to use half the number of particular hands to allow you to play other hand possibilities too? (Playing only 6 unsuited combos instead of all 12 would allow playing an extra pocket pair and still satisfy the right %.)
For this reason, starting hand charts typically vary from one teaching material to another. They will frequently have a similar % of hands in the range from each position.
But there is some leniency with how the hands are divvied up towards the bottom part of the range.
| Understanding %-based ranges can also help you better visualise which adjustments to make! |
A typical button opening range will account for around 40% of hands. But let’s say the players in the small blind and big blind are incredibly tight.
Now you’ll likely want to open anywhere from 50% of hands. Perhaps you can go all the way to 100% of hands (depending only on how tight they are).
- This scenario advocates the need for understanding combinatorics and how they interact with hand range charts.
Using them can help you get a better visual understanding of how to adjust your starting range.
How Combinatorics Affects Bluffing Frequencies
 How Combinatorics Affects Bluffing Frequencies
How Combinatorics Affects Bluffing Frequencies
Let’s suppose, after cbetting the flop and turn, you’ve now arrived at the river with a busted straight draw. (This scenario is often a perfect bluffing candidate in a triple-barrel spot.)
Before determining if you want to bluff this specific straight draw combo, you must ask a few questions:
- How many hands are you going to be value-betting?
- How many total busted straight draw combos do you have?
- What is the breakdown of how many suited/unsuited combos you have of that specific hand?
Now let’s take a lot at some helpful tips surrounding each question:
- Generally, you want about 2 or 2.5 value hands to every 1 bluff on the river. So, if you’ve picked out 40 value combos you’re betting for value, you should only have about 15 to 20 bluff combos.
- Imagine a board like Q-J-7-6-2. There’s a wide range of straight draws you might’ve continued to bet on the flop and turn with some frequency:
AK, AT, KT, T9, T8, 98, 95, 85, 84, 54, 53, 43
Assuming you have all combos, that equates to 12 x 16 = 192 total combos to bluff! Either you’ll need to value bet over 400 combos of hands (which is NOT going to happen!), or you need to be super-selective.
Ideal candidates might be those that block the value hands your opponent could have. (KT would block your opponent from having KQ and QT. These are two likely hands that might call you down, and you’d prefer your opponent NOT to have.)
- Let’s say you’re contemplating using 98 as a potential bluff candidate on the river (This play assumes you have a busted straight draw as well.) You should ask yourself, how many combos of 98 do you have in your entire range?
Do you have the suited versions AND the unsuited combos, or just the suited combos? If it’s only the suited hands, then you have 4 bluff combos. But if you have unsuited combos, too, then this suddenly adds 12 more bluffing combos!
So, be careful of bluffing too frequently (with too many combos). This factor especially crucial if you have off-suit combos of bluff candidates in your range, too.
Combinatorics: Poker Hand Probability Explained
In this section, we will take a look at some fast, easy poker combinatorics. These numbers show the many different possibilities of making some of the stronger hands in poker.
Poker Probability: 4-of-a-Kind Combinatorics
On paired boards, there is only going to be one combination of hands that makes quads. Assume that the A♣ and A♠ show up on the flop.
- Only one hole-card combo (A♦A♥) remains for players to make quads.
When there’s three-of-a-kind already on the board, though, this allows for many, many more combos of quads.
Multiply the one “quad card” needed by the remaining number of unknown cards in the deck (47 after the flop). You’ll see that it’s quite a lot more combos available than only the one with paired hole cards.
(Now, it’s not likely you’ll have all of these combos in your starting hand range. But this helps show how much probable it is to make quads with three-of-a-kind on the board.)
| Note: Ever wonder why most “high hands” and bad-beat jackpots require quads to use a pocket pair hand? As discussed, you’ll have significantly greater chances (combinatorically speaking, of course) of making quads on a Y-Y-Y board with X-Y (where X can be any card). With a pocket pair, you need one specific combo to make quads on a paired board! |
Poker Probability: Full House Combinatorics
For boats, let’s imagine a paired board like A-Q-8-8-3. Here are the following hands that can make full houses:
- A8 (6 combos) ==> (2 x 8’s remaining in the deck) x (3 x A’s remaining)
- Q8 (6 combos)
- 83 (6 combos)
- AA (3 combos)
- QQ (3 combos)
- 33 (3 combos)
So, there are 27 combos of full houses possible on this board. But not all combinations might be in a player’s hand range. It depends on their table position and action through the hand.
- For example, it’s unlikely that the preflop caller will have AA or QQ in their hand range, eliminating 6 boat combinations right away. They might not also call the flop and turn with pocket 3’s if there was betting on both streets.
Also, 83 (suited or not) will rarely be in any players hand range. Q8 and *maybe* A8 as well might not have all the off-suit combos in a player’s starting hand range.
It’s always essential to analyse which player in the hand has more of these “strong hand” combinations available in their range. So, you can determine who has a slight range and/or nut advantage.
Poker Probability: Flushes Combinatorics
Calculating combinatorics with flushes makes things interesting. It can be challenging to gauge precisely how many suited hand combos in a player’s range. (Some live players play ALL their suited hands!). And exactly how they split them up into the different betting lines, post-flop, is tricky to pin down.
In any case, say the community cards bring 3 cards of the same suit. This leaves 10 other cards in the suit available to help and make a flush.
Let’s take 10 cards x 9 cards and divide by 2 (because 8♥7♥ is the same as 7♥8♥, for example). Now, we see that there are 45 different possible combinations available once the 3-flush comes on the board (assuming A-K-Q of the same suit, in this case):
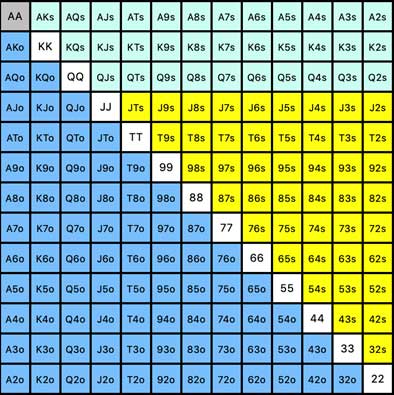
As mentioned previously, not all 45 combinations of flushes might be in the opponents’ range. Imagine a possible 6max UTG open range, for example, which only contains 15% of hands:
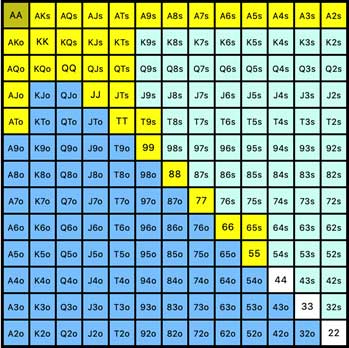
On a 3-flush board of A-K-Q, only 3 combinations of hands (JTs T9s, and 65s) provide the player with flushes.
But if the board is more like 8-7-4, all one suit, then suddenly all the UTG player’s suited “flushing” combinations become unblocked.
- They’ll have 20 total flush combinations (8 non-nut flush and 12 nut flush combos).
As such, it’s critical to think of poker probability/combinatorics for flushes that correctly account for a player’s range of suited hands.
| Note: On a 4-flush board, you must account for the suited hole cards as well as the unsuited combos. These hands contain one card of the flush when calculating combos. |
Poker Probability: Straights Combinatorics
For the combinatorics/possibility of straights in poker, it gets a little bit more complex. There are usually multiple straight possibilities available to a player, depending on the board texture.
The most significant determining factor in how many straight combinations a player will have in their range depends on the following:
- The number of unsuited hand combos a player will have of the specific hand value that can make a straight.
For example, if the board is 9-8-6, T-7 will make the nut straight, accounting for 16 combos in total.
But say the player only has T7suited in their range and not T7offsuit. Then this factor will decrease their nut straight combos by 75% – from 16 down to just 4!
Be sure to remember this point when you’re betting as a bluff on the river. Say you mistakenly account for 12 extra combos of straights that you think you have.
Then you’ll be finding way more bluffs than you should include in your range, causing you to over-bluff.
FAQ Section
Q: How many total combos of hands are there in poker?
A: There are 1,326 different possible hole card combos you can be dealt in Texas Hold’em.
Q: How many combos of paired hands are there in poker?
A: There are 6 combos of each pocket pair, meaning across 13 different card values, there are 78 combos of pocket pairs. So, the chance of being dealt a pocket pair is 78/1326 = 5.9% (once every 17 hands).
Q: How many combos of unpaired hands are there in poker?
A: There are 16 combinations of each unpaired hand (4 suited, 12 unsuited). So, that there are 288 suited unpaired combos and 864 unsuited unpaired combinations of hole cards possible.
Q: How do I calculate combinatorics?
A: For an unpaired hand, you’ll take the number of available cards of one value and multiply it by the number of available cards of the other value.
For example, there are 16 combos of AQ. Multiply (4 x Aces) by (4 x Queens) to get the answer. If there is an Ace on the board, then this leaves 3 remaining Aces. So, allowing for that, multiply (3 x Aces) by (4 x Queens) to get 12 possible hole card combos of AQ.
Q: What’s the biggest tip in counting combos?
A: In combinatorics, be sure not to double count poker hands. For example, 8-7 of hearts is the same as 7-8 of hearts. So, in particular combinatorics calculations, you’ll need to divide your answer by 2 to account for this.
Poker Combinatorics – The Bottom Line
Hopefully, this article will have provided you with a simplified combinatorics poker “system” to calculate different hand combos in-game.
Use this to your advantage to step up your game in the following study areas:
- How poker ranges work
- How to calculate the likelihood of your opponents having specific poker hands in their range
- How to have the correct ratio of value to bluff combos, street by street, and more!
Until next time, good luck at the felts!


