Poker is very much a maths and statistics-based game. While winning isn’t always guaranteed, playing a strategy that is conducive to following correct poker probabilities and odds will undoubtedly increase your chances of success at the felts.
Poker strategy involves a part of the game that deals with calculating (1) outs (which help define percentages in poker), (2) pot odds, and (3) your equity in the pot. Although the three concepts go hand in hand, our main focus in this article will be to explore the first two.
We'll break down the odds in poker and the probabilities associated in the game to help you understand the likelihood of particular outcomes and also to teach you how to play poker with probability in mind.
Table of Contents
- Poker Hands Probability
- How To Find the Probability of Poker Hands
- Odds of Being Dealt Certain Hole Cards in Poker
- Odds of Flopping a Made Hand
- Improving Your Draws
- What are Pot Odds in Poker?
- How to Read Pot Odds
- Pot Odds Formula
- How do Pot Odds Work
- Basic Rules of Poker Probabilities
- How to Convert Pot Odds into Percentages
- When to Call Using Pot Odds
- How to Calculate Pot Odds in Texas Hold’em
- How to Calculate Pot Odds in Omaha
- What If I Wanted To Practice Poker Probability Myself?
Poker Hands Probability
There are 2,598,960 distinct 5-card hands that can be made/dealt in poker. Let’s take a closer look at how these combinations break down into the various ranks of hands that one can attain in this poker probability chart:
Poker Hand
| Frequency (Distinct Hands) | Probability (%) | Odds (~) | |
|---|---|---|---|
| Royal Flush | 4 | 0.000154% | 1 in 649,740 |
| Straight Flush | 36 | 0.00139% | 1 in 72,193 |
| 4-of-a-Kind | 624 | 0.0240% | 1 in 4,165 |
| Full House | 3,744 | 0.1441% | 1 in 694 |
| Flush | 5,108 | 0.1965% | 1 in 509 |
| Straight | 10,200 | 0.3925% | 1 in 255 |
| 3-of-a-Kind | 54,912 | 2.1128% | 1 in 47 |
| Two Pair | 123,552 | 4.7539% | 1 in 21 |
| One Pair | 1,098,240 | 42.2569% | 1 in 2.4 |
| High Card | 1,302, 540 | 50.1177% | 1 in 2 |
There are a few things to note from this poker probability table:
- The ranking of hands goes up sequentially from the easiest hand to make to the most difficult (unlikeliest) one to have. (Therefore, now you know precisely why flushes rank higher than straights in Texas Holdem.)
- The probability of a pair in poker is ~42%.
- The chances of making a full house poker probability is less than 1% (~0.1441%)
- The probability in poker Texas Hold’em of making a royal flush is just 1 in 649,740 hands!
- The likelihood of a straight flush in poker is 1 in 72,193 hands or 0.00139%.
Please refer to this chart when determining how likely it is for specific poker hands to appear for you in a game.
How To Find the Probability of Poker Hands
- What is the probability of getting a two pair in poker?
- What is the possibility of being dealt a straight in poker?
- What is the likelihood of a full house in poker?
Within our vast 888poker Magazine, we have a plethora of articles that already include all the answers to your burning questions about probabilities and odds regarding specific poker hands.
Check them out using the links below:
- Royal Flush Odds
- Straight Flush Odds
- Four-of-a-Kind Odds
- Full House Odds
- Flush Odds
- Straight Odds
- Three-of-a-Kind Odds
- Two Pair Odds
- One Pair Odds
- High Card Odds
Odds of Being Dealt Certain Hole Cards in Poker
Multiply 52 cards in a standard deck by 51 (for the second card) and then divide this product by 2 (because A♣K♠ is the same thing as being dealt K♠A♣ – just the order it’s dealt in is reversed). You’ll see that there are 1,326 unique 2-card combinations you could receive in Texas Hold’em.

Breaking this down further, if you take a hand like AK, you can multiply the 4 Aces by 4 Kings to see that there are 16 combinations of AK total, both suited an unsuited.
Of these 16 combos, as there are 4 suits in poker, 4 of these AK combinations will be suited, leaving there to be 12 unsuited combinations of unpaired hands. (The same figures go for any non-paired poker hands). For pocket pairs, there will be 6 combinations of each value.
Knowing the above information, we can then do some basic maths to determine the likelihood of getting certain combinations of hole cards.
For example, for Pocket Aces, we would divide 6 combinations by 1,326 total combinations to see that we’ll receive this hand every 1 in 221 hands, on average.
For any specific suited hand, because there are only 4 combos of each holding (instead of 6 like with the pocket pairs), you’ll receive suited non-paired hands (of specific values) less frequently than you will pocket pairs. Therefore,you’ll be dealt a hand like AKs specifically every 1 in 332 hands, on average, meaning you’ll be dealt AA more frequently than you will AKs.
For the last point of this section, if you wanted to figure out the chances of being dealt hand X or better, simply add the number of combinations together for each holding.
For example, if we wanted to find the chances of being dealt QQ+ and/or AK, we’ll see that there are 18 pocket pair combos and 16 combos of AK, making for 34 combos total.
Dividing 1,326 total combos by 34 of these specific combos then means you’ll be dealt AK or QQ+ about 1 in every 39 hands.
Here’s a chart summarizing this essential hole card information outlined above, in addition to containing other probabilities for being dealt combinations of particular holdings:
| Hand | Total Hand Combinations | Probability (%) | Odds |
|---|---|---|---|
| Any 2 Cards | 1326 | 100% | 1 in 1 |
| AK (any specific hand) | 16 | 1.2% | 1 in 82.8 |
| AKs (any specific suited hand) | 4 | 0.3% | 1 in 331.5 |
| AKo (any specific off-suit hand) | 12 | 0.9% | 1 in 110.5 |
| AA (any pocket pair) | 6 | 0.5% | 1 in 221 |
| KK+ | 12 | 0.9% | 1 in 110.5 |
| QQ+ | 18 | 1.4% | 1 in 73.7 |
| JJ+ | 24 | 1.8% | 1 in 55.3 |
| TT+ | 30 | 2.3% | 1 in 44.2 |
| QQ+, AK | 34 | 2.5% | 1 in 39 |
| JJ+, AK | 40 | 3.0% | 1 in 33.2 |
| TT+, AK | 46 | 3.4% | 1 in 28.8 |
| Any Unpaired, Suited Cards | 312 | 23.5% | 1 in 4.3 |
| Any Unpaired, Unsuited Cards | 936 | 70.6% | 1 in 1.4 |
| Any Pocket Pair | 78 | 5.8% | 1 in 17 |
| Any Suited Connectors | 52 |
3.9% | 1 in 25.5 |
Odds of Flopping a Made Hand
The above section dealt with the likelihood of getting certain combinations of hole cards. But, what about poker odds on how those hole cards will improve (and to what degree) on specific flops?
Here’s a chart of various poker hole card probabilities to sift through and get accustomed to regarding the chances of flopping a made hand (of varying strengths):
| Your Hole Cards | Flop (Your Hand) | Probability (%) | Odds |
|---|---|---|---|
| Unpaired Cards | A Pair | 29.0% | 1 in 3.5 |
| Pocket Pair | A Set | 11.8% | 1 in 8.5 |
|
Connected Cards (JT thru 54) |
A Straight | 1.3% | 1 in 77 |
| Suited Connectors | A Flush | 0.8% | 1 in 119 |
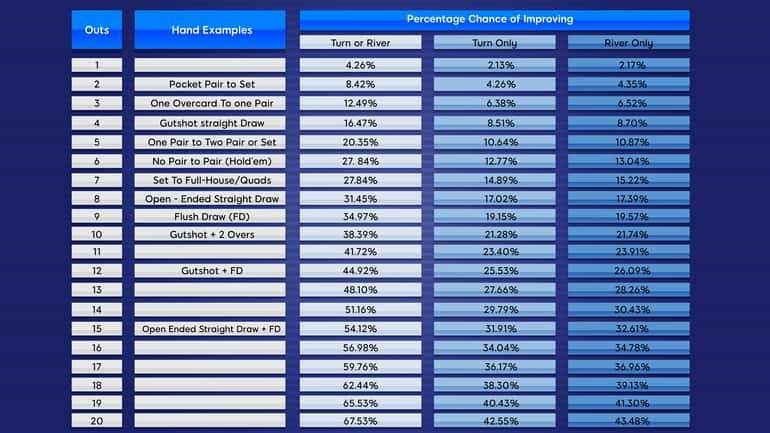
Poker Odds: Improving Your Drawing Hands
An “out” in poker is a card that will help improve the strength of your hand. The most frequent of outs are those that will help a player make a straight or a flush.
Here’s a table that explains the odds of improving your hand, depending on the number of outs you have:
What are Pot Odds in Poker?
Pot odds in poker take into account the number of "outs" you have (poker cards that can improve your hand), relating them to the amount of money you have to place (call) to see another card.
This calculation is used to determine whether calling to "chase" your draw is a profitable play in the long run. So, when players ask the question “Do pot odds matter?” - the answer is a big and very expressive YES!
Remember that poker is a game that is more about winning in the long run than in short, one-on-one sessions. Using the following information about pot odds, you can then make many +EV decisions at the tables.
How to Read Pot Odds
If you have a 33% chance of improving your hand, that percentage can be expressed as "1/3". For every three times you call to try to improve, you will complete your hand one of those times (on average).
However, it is necessary to convert these fractions into ratios in order to be able to relate them to pot odds.
In poker, these odds are expressed in the following format when trying to improve your hand:
Number of times you will not complete your hand
-------------------------------------------------------
Number of times you will complete your hand
An example of this would be 2:1 (which would be read as "2 to 1").
It can also be expressed as 33% (percentage) = 1/3 (fraction) = 2:1 (ratio).
Pot Odds Formula
Now that we understand ratios in relation to the odds of improving our poker hand, let's apply the same concept to understanding pot odds.
Let's say there's $50 in the main pot and someone bets an additional $50. There is now a total of $100 in the pot and you will have to call a bet of $50.
The pot odds in this scenario are $100 to $50, or 2 to 1.
The formula to determine this is as follows:
existing $ in the main pot + $ put into the pot during the current betting round
------------------------------------------------------------------------------
$$$ you have to pay (call)
For another example, let's assume that there is already $200 in the main pot. In this betting round, Player 1 bets $100, Player 2 calls $100, and now it's your turn to act.
What are your pot odds?
Using the formula above, we arrive at the following equation: $400 : $100 or 4 to 1
($200 in the main pot) + ($200 from this betting round)
-----------------------------------------------------------
($100 that you have to pay (call))
How do Pot Odds Work

The next step in determining whether or not we have the correct pot odds to call relates the pot odds we calculated to the possibilities of improving our hand. (We'll learn exactly how to calculate our odds of improving in the next chapter.)
Simply put, if our odds of improving to a winning hand are greater than the pot odds we are getting to call, then calling becomes the right and most profitable play.
Let's say we're playing Texas Hold'em and we have 8-7 off suit. The board is K-5-6-2 rainbow. Currently, our hand value is extremely weak (8-high), but we have the possibility to make the best possible straight (nut straight) if a 4 or 9 comes on the river.
With a standard deck of 52 cards, we already know 6 of those cards on the turn (2 in our hand and 4 on the board). So, out of the 46 cards left in the deck that can be dealt on the river, only 8 of them will improve our hand (4 fours and 4 nines). This calculation can be expressed as a fraction of 8/46.
We can then use this ratio to relate “river cards that won't improve our hand” to “river cards that will, in fact, improve our hand”:
- 8 cards on the river will help
- 46 unknown cards - 8 cards that will help us = 38 cards that won't help us
- 38 Cards That Won't Help Us : 8 Cards That Will Help Us
- 38:8
- 4.75:1
The ratio of 4.75 to 1 indicates that for every 4.75 times we don't improve, we improve once. So, to make a profitable call here, we need to have pot odds greater than 4.75 to 1 (ie. $500 already in the pot against a bet of $100).
Basic Probability Rules Poker
Now, of course, it’ll be difficult to refer to this chart for every hand to see what chances you’ll have of improving and then relate this to the pot odds you’re getting. So, to give you a basic shortcut, use the following trick to help you with how to calculate the probability of your poker hands improving:
If you multiply the number of outs you have on the flop by 4, you’ll get a solid approximation for the chances of making your hand by the turn or river (i.e. with two cards to come).
If you multiply the number of outs you have on the flop or the turn by 2, you’ll get a reliable approximation for the chances of making your hand on the very next card.
Sometimes, you’ll want to vary perhaps the number of outs that will help you improve your hand, to account for the chances of it also helping your opponent improve to an even better hand.
For example, if you think your opponent might have a higher flush draw or if the board pairs giving you a flush and your opponent perhaps a full house, you might lessen your “outs” slightly (e.g. 8.5 outs instead of 9). This adjustment will account for this possibility, when relating it to your pot odds and how you should proceed in the hand.
How to Convert Pot Odds into Percentages
Now that we've learned how to calculate pot odds and the odds of improving, it's time to put the two together to see if we have the right odds to call.
However, when using the “Rule of 2 and 4”, you will be left with a percentage, whereas when calculating pot odds, you will be left with a ratio (such as 2 to 1 or 2:1)
Thus, it is important to be able to convert percentages into ratios and vice versa if you want to quickly determine whether or not you are getting the right value for the call.
Let's start by learning how to convert percentages to ratios.
PERCENTAGES TO PROBABILITIES:
Using the “Rule of 2 and 4”, with 9 outs and 2 cards to come, we have about a 36% chance of improving our hand to a flush. Through a simple calculation, we can conclude that, approximately 64% of the time, we do not complete our draw.
When converting percentages to ratios, you should always put them in the following format:
(probability of not improving your hand) : (probability of improving your hand)
Using this format will leave us with a ratio of 64:36, or around 2 to 1 - a ratio that can easily be compared to our pot odds. The more you practice this process (pot odds vs percentage), the better your ability to determine the odds of improving your hand.
PROBABILITIES TO PERCENTAGES:
Let's turn things around a bit and see how we can turn pot odds into percentages. Let's say someone makes a ½ pot bet, which would give us 3 to 1 on a call (someone would bet $50 into a $100 pot. The pot is now $150 and you will have to call $50 if you want to call, getting pot odds of 3 to 1).
By transforming this ratio into a fraction, we can easily calculate the percentage, as we will see below:
(price you need to call / price you need to call + money already in the pot)
In this example, the price we must pay is $50. So, the (price we have to call) + (the money already in the pot) would be $50 + $150, giving us a fraction of $50/$200.
50/200 = 0.25 which can easily be converted into a 25% percentage by multiplying 0.25 by 100.
This percentage, relative to the strength of your hand, means that you would need to have more than a 25% chance of winning the hand to make a profitable call.
If this still seems difficult to you, don't worry! The more you practice calculating odds, the better you will get.
To help you, we replicated the table above and added ratio odds already calculated for you!
| 1 CARD TO COME |
2 CARDS TO COME |
||||||
|---|---|---|---|---|---|---|---|
| FLOP to TURN | TURN to RIVER |
TURN & RIVER |
|||||
| OUTS | HAND EXAMPLES | % | ODDS | % | ODDS | % | ODDS |
| 1 | 2.13% | 45.95 : 1 | 2.17% | 45.08 : 1 | 4.26% | 22.50 : 1 | |
| 2 | Pocket Pair to Set | 4.26% | 22.47 : 1 | 4.35% | 21.99 : 1 | 8.42% | 10.88 : 1 |
| 3 | 1 Overcard to 1 Pair | 6.38% | 14.67 : 1 | 6.52% | 14.34 : 1 | 12.49% | 7.01 : 1 |
| 4 | Gutshot Straight Draw | 8.51% | 10.75 : 1 | 8.70% | 10.49 : 1 | 16.47% | 5.07 : 1 |
| 5 | 1 Pair to 2 Pair or Set | 10.64% | 8.40 : 1 | 10.87% | 8.20 : 1 | 20.35% | 3.91 : 1 |
| 6 | No Pair to Pair (Hold'em) | 12.77% | 6.83 : 1 | 13.04% | 6.67 : 1 | 24.14% | 3.14 : 1 |
| 7 | Set to Full-House / Quads | 14.89% | 5.72 : 1 | 15.22% | 5.57 : 1 | 27.84% | 2.59 : 1 |
| 8 | Open-Ended Straight Draw | 17.02% | 4.88 : 1 | 17.39% | 4.75 : 1 | 31.45% | 2.18 : 1 |
| 9 | Flush Draw | 19.15% | 4.22 : 1 | 19.57% | 4.11 : 1 | 34.97% | 1.86 : 1 |
| 10 | Gutshot + 2 Overcards | 21.28% | 3.70 : 1 | 21.74% | 3.60 : 1 | 38.39% | 1.60 : 1 |
| 11 | 23.40% | 3.27 : 1 | 23.91% | 3.18 : 1 | 41.72% | 1.40 : 1 | |
| 12 | Gutshot + Flush Draw | 25.53% | 2.92 : 1 | 26.09% | 2.83 : 1 | 44.96% | 1.22 : 1 |
| 13 | 27.66% | 2.62 : 1 | 28.26% | 2.54 : 1 | 48.10% | 1.08 : 1 | |
| 14 | 29.79% | 2.36 : 1 | 30.43% | 2.29 : 1 | 51.16% | 0.95 : 1 | |
| 15 | Open-Ended Straight Draw + FD | 31.91% | 2.13 : 1 | 32.61% | 2.07 : 1 | 54.12% | 0.85 : 1 |
| 16 | 34.04% | 1.94 : 1 | 34.78% | 1.88 : 1 | 56.98% | 0.76 : 1 | |
| 17 | 36.17% | 1.76 :1 | 36.96% | 1.71 : 1 | 59.76% | 0.67 : 1 | |
| 18 | 38.30% | 1.61 : 1 | 39.13% | 1.56 : 1 | 62.44% | 0.60 : 1 | |
| 19 | 40.43% | 1.47 : 1 | 41.30% | 1.42 : 1 | 65.03% | 0.54 : 1 | |
| 20 | 42.55% | 1.35 : 1 | 43.48% | 1.30 : 1 | 67.53% | 0.48 : 1 |
When to Call Using Pot Odds

If we can determine the number of outs we have to improve our hand, then using the chart above we can easily know the odds in any given situation.
From there, we simply compare those odds to the pot odds. If your odds of improving are better than the pot odds, then you have the correct pot odds to call.
To simplify it even further, when comparing the numbers in your ratio, if the number to the left of your pot odds ratio is greater than the number to the left of your ODDS OF IMPROVEMENT ratio - then you should go ahead and call!
To illustrate this point, let's use this brief example:
You have 6 outs and only the river card to come. There is $500 in the main pot and you are betting $100.
Do you have the right pot odds to call?
First of all, it is necessary to calculate our probabilities of improving our hand.
In the poker chart above, we can see that these odds are 6.67 to 1 (when there are 6 outs).
Second, we have to determine our pot odds. Take the $500 from the main pot and add it to your opponents' $100 bet. That's $600 that you could win by calling the $100 bet.
So, your pot odds are 6 to 1.
- Pot Odds: 6:1
- Odds of improving: 6.67 to 1
As the number on the left (displayed in bold) for the pot odds is NOT greater than our odds of improving (6–6.67), we do NOT have clear enough pot odds to call.
However, just because you don't have the right pot odds to call, doesn't mean you should always fold your hand when facing that bet. Likewise, when you have the right pot odds, it doesn't mean you should always call.
There are other considerations you should make before folding your hand.
Let's go a little deeper into some of them.
Additional Notes
- Call on the Flop: Remember that if you call on the flop and don't complete your draw on the turn, you could still face another bet on the turn. This scenario could affect how you use the "Rule of 2 and 4" in your calculations, as you would also not see the free card on the river.
- Other players behind you: The other players who have yet to act can also call, or potentially even raise! If you think they might call, you can take that into account when determining your pot odds. If you think they might raise, a fold might actually be the best move.
- Fold Equity: Pot odds generally refer to whether or not calling with a draw is a profitable play. However, you should always balance your hand range and consider other possibilities as well - one of them being raising when it seems like a good solution. This play is considered a "semi-bluff", where you can win by (1) improving your hand on a later round; or (2) make your opponent fold immediately.
- Implied odds: Implied odds refer to how much money can be won on future betting rounds if you actually complete your draw. For example, people with a flopped straight or flush draw often don't have the correct expressed pot odds to profitably call a bet to see if they'll hit the draw on the turn or river. However, if they complete the draw, they usually pin their hopes on winning another bet or two on future streets to make up the call difference without first having the proper, well-expressed odds.
- Equity vs. Villain's Range: Pot Odds vs. Equity - this is a concept that not all poker players can differentiate. While the term “pot odds” refers to whether or not you get the right price to call, equity refers to how much pot money should be yours based on the percentage of times your hand will win against the hand or a villain's range of hands.
What If I Wanted To Practice Poker Probability Myself?
The methodology behind practising poker probability problems without using shorthand can certainly still be done.
To do this, you need to add together the probabilities of specific outcomes occurring, for example:
- Hitting one of your outs on the turn
- Hitting one of your outs on the river, but not the turn
EXAMPLE PROBLEM #1: A Normal Flush Draw
To work through a typical poker probability problem, suppose you have a flush draw after the flop and want to simply know the chances of improving to a flush by the river.
With 4 of 13 cards of the suit being revealed already, there are 9 remaining cards (“outs”) that can help you.
And with two hole cards and three flop cards already accounted for, there are 47 unknown cards to you in the deck.
Knowing this, you can do the appropriate calculations and add the results together to determine your chances of making your flush:
- Odds of hitting your flush on the turn: (9/47) = 19.15%
- Odds of hitting your flush on the river: (39/47)*(9/46)= 16.23%
- Odds of making your flush on the turn OR the river: 19.15% + 16.23% = 35.38%
Here, you can see the odds of making a flush by the river after flopping a flush draw is 35.38%. If you take the “shortcut” rule outlined above, you can see that 9 outs multiplied by 4 equals 36%, which is pretty close to the exact answer here.
EXAMPLE PROBLEM #2: A Backdoor Flush Draw
To practice the probabilities of hitting a backdoor flush, you would have to multiply (10 flush outs /47 unknown cards) for the turn by (9 flush outs /46 unknown cards) on the river. The result would show that there’s a ~4.2% chance of a 3-flush on the flop becoming a full, 5-card flush by the river.
Calculating Probability of Poker Hands Heads-Up
One critical thing to note in poker is the difference in terms of equity spread when there is only one opponent versus multiple opponents in a poker hand with you.
Against many players, the equity of everyone’s respective hands is going to be lower than if it was heads-up because it’ll be divided and spread out among the other remaining players.
Take Pocket Aces for example. Against the following Villain range for your opponent(s) -
- Any pocket pair
- Any suited Ace
- Any two broadway cards
- Suited connectors: 54s to T9s
- One-gapped suited connectors: 86s to J9s
- Q9s, K9s
Here are the equity percentages that Pocket Aces has against:
- One opponent: 83.4%
- Two opponents: 70.6%
- Three opponents: 60.2%
- Four opponents: 51.4%
As you can see, the more opponents there are in a hand, the lower the chance AA has of winning, which is why it is so advantageous to have these big pairs play out in a heads-up, low SPR pot.
And for when you have drawing hands in a multi-way scenario, having more opponents may not change the number of outs you have to improve. However, the chances of someone else having a better draw than you or a hand that could later outdraw you certainly goes up with more opponents.
Additionally, when action is multi-way, it is essential to note that players tend to bluff less and bet more for value if they do bet.
Therefore, considering the last two points, it is crucial to always remember how many opponents are in a hand and determine the best way to go about playing accordingly.
Poker Probability Summary
To increase the probability of winning poker, you must become accustomed to the odds and probabilities that are presented to you in the game. Become familiar with outs and calculating your percentages of improving and be able to quickly relate these to the pot odds you may be getting, so that you can determine if you can call profitably or not.
(For more info on pot odds and bet sizing, check out this Comprehensive Bet Sizing Guide).
Remember also that you don’t always need to “just call” whenever you have a draw. Sometimes, it can be advantageous to bet or raise. This way, you can either win by improving later on to the best hand or getting your opponent to fold.
(See more about equity and fold equity here.)
In summary, and to quote The Hunger Games: “May the (poker) odds be ever in your favour!” Good luck at the felts!
Updated On: March 21, 2023


